MANDELBRÖT & JULIA SETS
MANDELBRÖT & JULIA SETS
This version allows you to draw the Mandelbröt sets for ten different iterative functions and their associated Julia sets.
| Function | Real part | Imaginary part |
| z = z² + c | x² - y² | 2xy |
| z = z³ + c | x³ - 3xy² | 3x²y - y³ |
| z = z² + z + c | x² - y² + x | y(2x + 1) |
| z = z² - z + c | x² - y² - x | y(2x - 1) |
| z = z(z² - 1) + c | x³ - 3xy² - x | 3x²y - y - y³ |
| z = z²(z - 1) + c | x³ - x² - 3xy² + y² | 3x²y - 2xy - y³ |
| z = z² - z - 1 + c | x² - y² - x - 1 | y(2x - 1) |
| z = z⁴ + c | x⁴ - 6x²y² + y⁴ | 4(x³y - xy³) |
| z = z(z + i) + c | x² - y² - y | x(2y + 1) |
| z = z²(z + i) + c | x³ - 3xy² - 2xy | 3x²y + x² - y² - y³ |
Areas for enlargement are selected by dragging the mouse over a display and displays can be printed and stored, either as the basic data used to generate the display or as the actual display data.
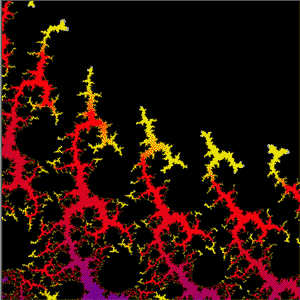
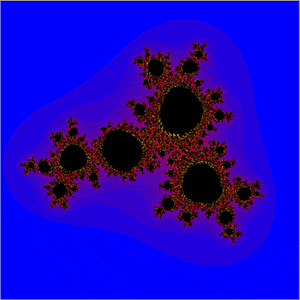
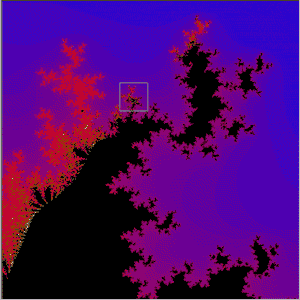
The illustrations are areas of the sets produced by the function z = z²(z - 1) + c
A sample storage file is included in the package and there is also an extensive "Help" file appended.
The current version has had a number of modifications added, the most important of which is that you can now enter your own equations.
Other Mandelbröt sites:-