The MANDELBRÖT & JULIA GALLERY, page 2 

The description lists the type of set, (Mandelbröt or Julia), the function used to generate the set and the scan area parameters,
(the coordinates of the lower-left corner, followed by the length of the side). The constant is added for Julia sets.
Most values are shown in exponential notation.
Click the thumb-nail graphic for an enlarged version.

Mandelbröt 1 Mandelbröt
z = z(z + i) + c
(-2.5, -2.5),
4.00 		Mandelbröt 2 Mandelbröt
z = z(z + i) + c
(-3.47E-2, -1.90),
1.42E-1
 Mandelbröt 3 Mandelbröt
z = z(z + i) + c
(7.32-2, -1.20),
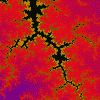
1.00E-2 		Mandelbröt 4 Mandelbröt
z = z(z + i) + c
(8.13E-2, -1.02),
4.49E-4
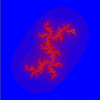
Julia 1 Julia
z = z(z + i) + c
(-2.00, --2.50),
4.00
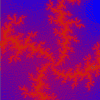
(0.0816, -1.0176i) 		Julia 2 Julia
z = z(z + i) + c
(8.66E-1, 2.12E-1),
1.05E-1
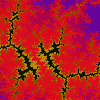
(0.0816, -1.0176i) 		Julia 3 Julia
z = z(z + i) + c
(9.62E-1, 2.45E-1),
2.91E-3
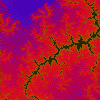
(0.0816, -1.0176i) 		Julia 4 Julia
z = z(z + i) + c
9.64E-1, 2.48E-1),
8.51E-5
(0.0816, -1.0176i)
Mandelbröt 5 Mandelbröt
z = z²(z + i) + c
(-1.80, -2.20),
3.60
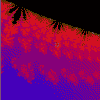
 Mandelbröt 6 Mandelbröt
z = z²(z + i) + c
(-1.85E0-1, -1.041),
7.77E-2
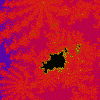
 Mandelbröt 7 Mandelbröt
z = z²(z + i) + c
(-1.43E-1, -9.98E-1),
2.51E-3
 Mandelbröt 8 Mandelbröt
z = z²(z + i) + c
-1.41E-1, -9.99E-1),
1.16E-4
Julia 5 Julia
z = z²(z + i) + c
(-1.50, -1.80),
3.00
(-0.1413, -0.9976i)
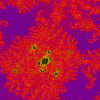
 Julia 6 Julia
z = z²(z + i) + c
(7.70E-1, -1.51E-1),
1.02E-1
(-0.1413, -0.9976i)
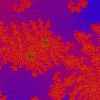
 Julia 7 Julia
z = z²(z + i) + c
(8.48E-1, 1.88E-1),
4.54E-3
(-0.1413, -0.9976i)
 Julia 9 Julia
z = z²(z + i) + c
8.49E-1, 1.90E-1),
3.43E-4
(-0.1413, -0.9976i)