Graph Gallery, page 1 

The descriptions list the function/s which produced the graph and the range of the variable/s used.
Click a thumb-nail graphic for an enlarged version.
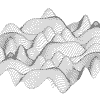
z=f(x,y) graph 1 z = Cos(x+2*pi*cos(y/2))+Cos(y+2*pi*Cos(x/2))
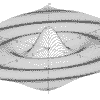
x = -9 to 9, y = -9 to 9		 Psuedo-Bessell function z = (x*x-y*y)^2/(x*x+y*y)
x = -9 to 9, y = -9 to 9
Psuedo-Bessell function
Solid surface, Psuedo-Bessell function Surface plot of z = 4*(x*x-y*y)^2/(x*x+y*y)
x = -5 to 5, y = -5 to 5
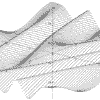
Psuedo-Bessell function		 z=f(x,y) graph 2 z = Cos(x+2*pi*Cos(y/2))
x = -2pi to 2pi, y = -2pi to 2pi
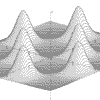
z=f(x,y) graph 3 z = Exp(Sin(x)*Sin(y)*3)/4
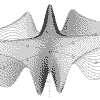
x = -2pi to 2pi, y = -2pi to 2pi 		z=f(x,y) graph 4 z = Cos(x*x-y*y)
x = -pi to pi, y = -pi to pi
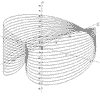
x=f(t), y=f(t), z=f(t) 1 x = 2*Cos(t) + Sin(2*t)
y = Sin(t) + Cos(2*t)
z = t*Cos(t)/10
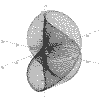
t = -30 to 30 		x=f(t), y=f(t), z=f(t) 2 x = 2*Cos(t) + Cos(2*t)
y = 2*Sin(t) + Sin(2*t)
z = t*Sin(t)
t = -50 to 50
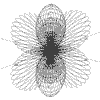
r=f(a,b) 1 r = Sqr(4*Cos(a + b))
a = 0 to 2pi, b = 0 to 2pi 		r=f(a,b) 2 r = Sin(2*a) + Sin(2*b)
a = 0 to 2pi, b = 0 to 2pi
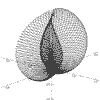
r=f(a,b) 3 r = Sin(a) + Sin(b)
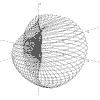
a = -pi to pi, b = -pi to pi 		r=f(a,b) 4 r = 1/Sqr(a*a + b*b)
a = 0 to 2pi, b = 0 to 2pi
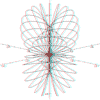
Red/blue anaglyph Red/blue anaglyph
r = sin(a + b) - cos(a + b) a = 0 to 2pi
b = 0 to 2pi 		x=f(t), y=f(t) 1 x=cos(t) + t^2*sin(t)
y=sin(t) + t^2*cos(t)
t = -8pi to 8pi
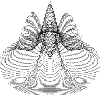
z=f(r,a) z = e^(-r*r)*(sin(2*r)-r*cos(4*a))
r = 0 to 2
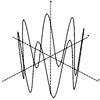
a = -2pi to 2pi 		r-f(t), a=f(t), z=f(t) r =2
a = t
z =cos(7*t)
t = -pi to pi